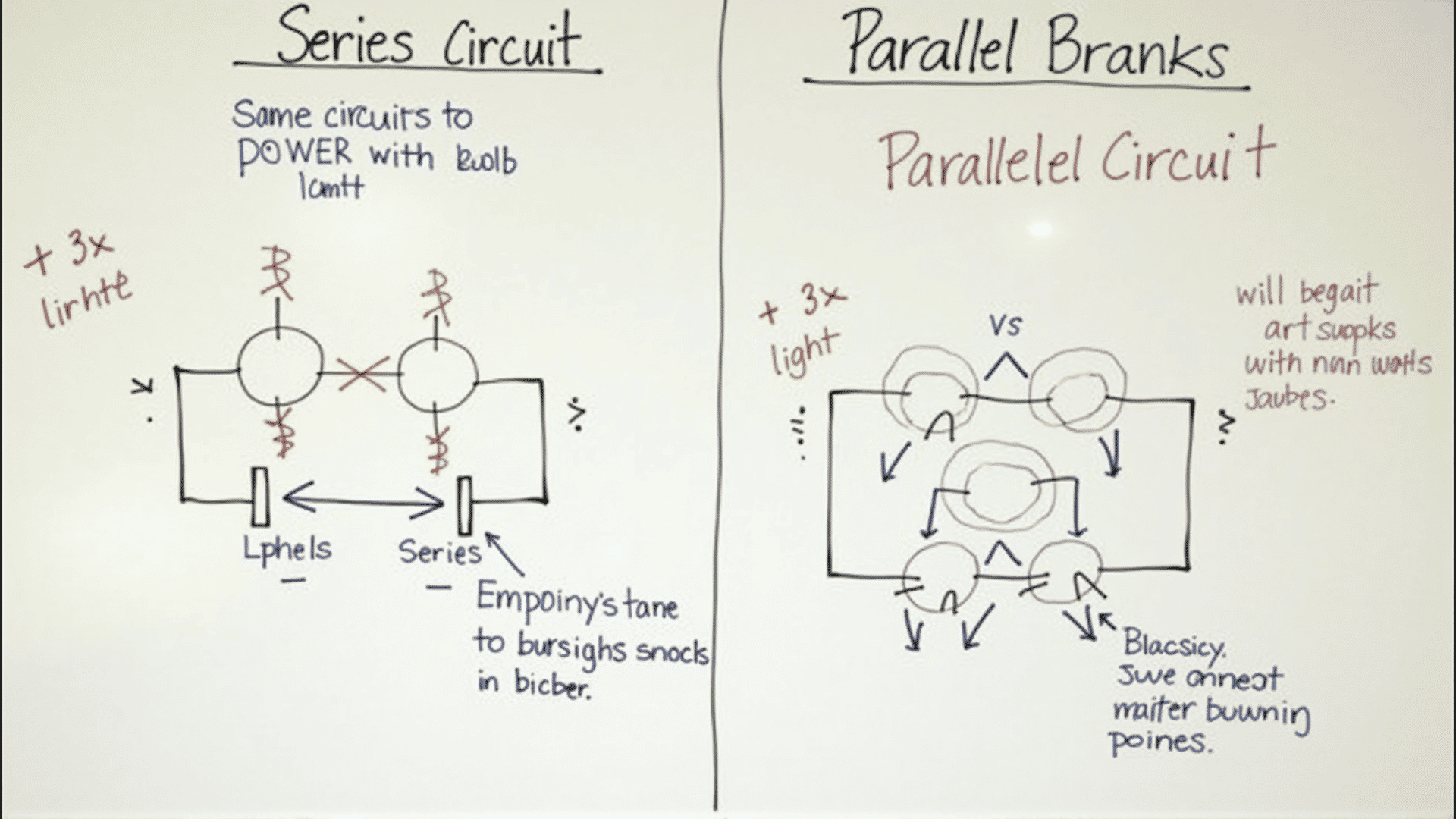
When exploring the world of electronics, two fundamental types of electrical circuits frequently encountered are series and parallel circuits. Understanding these configurations is crucial for anyone involved in electrical or electronic activities.
In a series circuit, components are connected end-to-end, providing a single path for the flow of electric current. Each component experiences the same current, but the voltage across each component can vary. One distinguishing characteristic of series circuits is that if a single component fails, the entire circuit is interrupted, much like how the removal of a single bulb from a string of holiday lights can cause the entire strand to go dark.
Calculating total resistance in a series circuit is straightforward. The total resistance, denoted as ( R_t ), is simply the sum of the resistances of the individual components. Mathematically, this is expressed as:
[ R_t = R_1 + R_2 + R_3 + \ldots + R_n ]
Here, ( R_1, R_2, R_3, \ldots, R_n ) represent the resistances of each component in the circuit.
Conversely, a parallel circuit offers multiple paths for the electric current to flow. Each component is connected across the same voltage source, meaning that all components receive the same voltage. However, the current passing through each component can differ, depending on their resistance values. A key advantage of parallel circuits is their robustness; if one component fails, the remaining components can still operate effectively, as the circuit remains intact through alternative paths.
Calculating total resistance in a parallel circuit is more complex than in a series circuit. The total resistance for resistors in parallel can be determined using the formula:
[ \frac{1}{R_t} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \ldots + \frac{1}{R_n} ]
After computing the reciprocal sum, ( R_t ), the total resistance, can be found by taking the reciprocal of the result obtained from this summation.
Both series and parallel circuits have their unique applications and are often used in combination to design complex electrical systems. Understanding how they function individually and collectively is key to mastering electronic circuit design and analyzing electrical networks.